直线对称是数学中一个重要的概念,它在几何中具有广泛的应用。本文将深入探讨直线对称的性质,并展示它在不同领域的应用。通过学习直线对称,我们将更好地理解几何问题,并能够应用它解决实际问题。

直线对称的基本概念
1.1直线对称的定义与特点
直线对称是指图形相对于一条直线保持对称。这种对称性质具有一些重要的特点,如对称性、不变性等。

1.2直线对称的判定方法
要判定一个图形是否具有直线对称性,我们可以通过观察其构造,寻找可能的对称轴,并验证对称性。
直线对称的性质和定理
2.1直线对称的性质
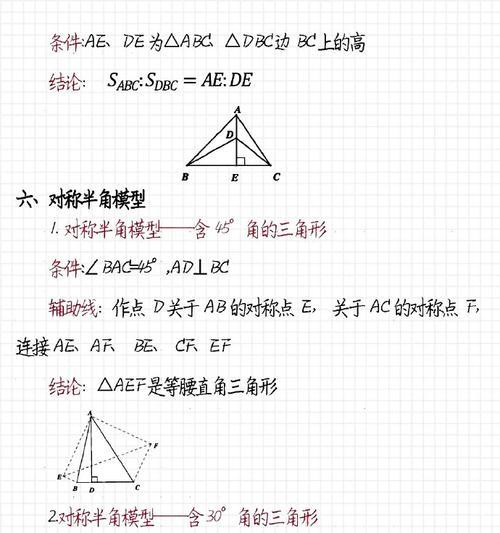
直线对称具有一些重要的性质,如保持长度不变、保持角度大小不变等。这些性质使得直线对称在几何推理和证明中起到重要作用。
2.2直线对称的定理
直线对称还有一些重要的定理,如直线对称传递性、直线对称与圆的关系等。这些定理为我们解决几何问题提供了有效的工具。
直线对称在几何推理中的应用
3.1直线对称在证明中的应用
直线对称可以作为证明中的一个重要工具,通过利用对称性质,我们可以更容易地推导出结论,简化证明过程。
3.2直线对称在构造中的应用
直线对称在构造几何图形时也具有重要作用。通过利用对称性质,我们可以更精确地定位点、直线或图形的位置,完成准确的构造。
直线对称在实际问题中的应用
4.1直线对称在建筑设计中的应用
直线对称在建筑设计中被广泛应用,如建筑立面的设计、镜像艺术等。通过利用直线对称,设计师可以创造出更具美感和均衡感的建筑作品。
4.2直线对称在生物学中的应用
直线对称在生物学中也有一定的应用,如研究生物体的形态和结构。通过观察生物体的直线对称性质,科学家可以推断其生长和发展的规律。
直线对称的拓展与扩展
5.1直线对称的三维应用
除了在二维平面中,直线对称性质还可以拓展到三维空间。在三维几何中,直线对称可以帮助我们理解物体的旋转和镜像等现象。
5.2直线对称的数学推广
直线对称性质还可以推广到更高阶的数学领域,如群论和代数结构中的对称性。这种推广为我们深入研究数学提供了更多的可能性。
通过本文的介绍,我们了解了直线对称的基本概念、性质和定理,以及它在几何推理和实际问题中的应用。直线对称不仅是数学中的重要概念,也在各个领域具有广泛的应用。通过深入学习直线对称,我们可以提高数学思维能力,并能够将其运用到实际问题中,解决现实生活中的难题。